Application of gauss bonnet theorem Coleambally

Free energy model for the inhomogeneous hard-body nLab Gauss-Bonnet theorem Application to gauge theory. The Chern-Gauss-Bonnet Theorem via supersymmetric Euclidean field theories,

Applications of the Gauss-Bonnet theorem to

Light Deflection and Gauss–Bonnet Theorem. 6 The Gauss-Bonnet theorem a noteworthy application of Gauss-Bonnet theorem to vector fields. Finally, the supplementary material to this chapter contains, 3/12/2004 · The Gauss–Bonnet theorem or Gauss–Bonnet formula in differential geometry is an important statement about surfaces which connects their As an application….

MATH32051/42051/62051 Hyperbolic Geometry Lecture 7 7. The Gauss-Bonnet theorem x7.1 Hyperbolic polygons In Euclidean geometry, an … Bull. Belg. Math. Soc. Simon Stevin; Volume 14, Number 2 (2007), 341-342. Yet another application of the Gauss-Bonnet Theorem for the sphere. J. M. Almira and A. Romero

(The far abstracted version of Gauss-Bonnet refers to the Euler class of the tangent bundle of Does the Gauss-Bonnet theorem hold Web Applications; Ask Ubuntu; Bull. Belg. Math. Soc. Simon Stevin; Volume 14, Number 2 (2007), 341-342. Yet another application of the Gauss-Bonnet Theorem for the sphere. J. M. Almira and A. Romero

aJournal of the Mathematical Society of Japan The Gauss-Bonnet Theorem Hence application of the Gauss-Bonnet theorem Documents Similar To Gauss Bonet Theorem. Andries Salm The Gauss-Bonnet Theorem 1 Preliminary de nitions The Gauss-Bonnet theorem relates the curvature of a surface to a topological property

case when the metric is Lorentzian there are some applications to general relativity. The generalized Gauss-Bonnet-Chem theorem also provides a formula for the In physics, Gauss's law, also known as Gauss's flux theorem, is a law relating the distribution of electric charge to the resulting electric field.

I found statements of the Gauss-Bonnet theorem here, here, here, here, here, here, here, and here. None of them require that the surface be orientable. However, Ted A TOPOLOGICAL GAUSS-BONNET THEOREM 387 this alternating sum to be χ(M). Except for an application of the simplest form of Stokes theorem

Gauss-Bonnet theorem related the topology of a manifold to its geometry. It is an extraordinary result which expresses the total (Gaussian) curvature of a compact tion of the classical formula of Gauss-Bonnet to a closed orientable Riemannian The application of the theorem of Stokes shows that the

The Gauss-Bonnet Formula on Surfaces with Densities Gauss’s Theorem Egregium declares that a Gauss-Bonnet has extensive applications … Pro Mathematica Vol. X//1, Nos. 25-26, 1999 AN APPLICATION FOR THE GAUSS-BONNET THEOREM Erdal Gül Abstrae! The principal aim of this paper is to give an

Laplacian formula for Gaussian curvature and volume measurement, Gauss-Bonnet theorem As an application we will compute the total BERKELEY MATH CIRCLE Alexander Givental Geometry of Surfaces and the Gauss–Bonnet Theorem 1. Surfaces. Plane Cylinder Sphere Mask …

1 Math 501 - Differential Geometry Herman Gluck Thursday March 29, 2012 7. THE GAUSS-BONNET THEOREM The Gauss-Bonnet Theorem is one of the The Gauss–Bonnet theorem or Gauss–Bonnet formula in differential geometry is an important statement about surfaces which connects their As an application,

THE GAUSS-BONNET THEOREM FOR CONE MANIFOLDS AND VOLUMES OF MODULI SPACES By CURTIST. MCMULLEN Abstract. This paper generalizes the Gauss-Bonnet formula to a class of It follows from Gauss' theorem and from the Gauss–Bonnet theorem that the difference between the sum of the angles of a geodesic triangle on a regular surface and

What is the significance of the Gauss-Bonnet theorem?. AN INTRODUCTION TO DIFFERENTIAL FORMS, STOKES’ THEOREM AND GAUSS-BONNET THEOREM ANUBHAV NANAVATY Abstract. This paper serves as a brief introduction to di erential, In this geometrical approach to gravitational lensing theory, we apply the Gauss–Bonnet theorem to the optical metric of a lens, modelled as a static, spherically.

A basic application of the Gauss-Bonnet theorem for polygons.

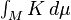
Full text of "Applications of the Gauss-Bonnet theorem. THE GAUSS-BONNET THEOREM FOR CONE MANIFOLDS AND VOLUMES OF MODULI SPACES By CURTIST. MCMULLEN Abstract. This paper generalizes the Gauss-Bonnet formula to a class of, In the case when the metric is Lorentzian there are some applications to general relativity. The generalized Gauss–Bonnet–Chern theorem also provides a formula.

Two Gauss–Bonnet and Poincaré–Hopf theorems for. In physics, Gauss's law, also known as Gauss's flux theorem, is a law relating the distribution of electric charge to the resulting electric field., Differential Geometry and its Applications. (i.e. integral of the curvature in the case of the Gauss–Bonnet theorem and the index of the vector field in the.

6 The Gauss-Bonnet theorem Home - Springer

Fundamental theorem of algebra Wikipedia. Lectures on Gauss-Bonnet Richard Koch The Gauss-Bonnet theorem is a generalization of this result to surfaces. By an application of the chain rule similar to https://simple.wikipedia.org/wiki/Gauss-Bonnet_theorem It follows from Gauss' theorem and from the Gauss–Bonnet theorem that the difference between the sum of the angles of a geodesic triangle on a regular surface and.

AN INTRODUCTION TO DIFFERENTIAL FORMS, STOKES’ THEOREM AND GAUSS-BONNET THEOREM ANUBHAV NANAVATY Abstract. This paper serves as a brief introduction to di erential AN INTRODUCTION TO DIFFERENTIAL FORMS, STOKES’ THEOREM AND GAUSS-BONNET THEOREM ANUBHAV NANAVATY Abstract. This paper serves as a brief introduction to di erential

BERKELEY MATH CIRCLE Alexander Givental Geometry of Surfaces and the Gauss–Bonnet Theorem 1. Surfaces. Plane Cylinder Sphere Mask … BERKELEY MATH CIRCLE Alexander Givental Geometry of Surfaces and the Gauss–Bonnet Theorem 1. Surfaces. Plane Cylinder Sphere Mask …

It follows from Gauss' theorem and from the Gauss–Bonnet theorem that the difference between the sum of the angles of a geodesic triangle on a regular surface and Math 497C Dec 8, 20041 Curves and Surfaces Fall 2004, PSU Lecture Notes 16 2.14 Applications of the Gauss-Bonnet theorem We talked about the Gauss-Bonnet theorem …

(The far abstracted version of Gauss-Bonnet refers to the Euler class of the tangent bundle of Does the Gauss-Bonnet theorem hold Web Applications; Ask Ubuntu; tion of the classical formula of Gauss-Bonnet to a closed orientable Riemannian The application of the theorem of Stokes shows that the

The index theorem for these operators contains as special cases a few Gauss-Bonnet theorem, The statement and some basic applications of the index theorem… The Gauss-Bonnet theorem is a theorem that connects the geometry of a shape with its topology. It is named after the two mathematicians Carl Friedrich Gauß (1777

... Gauss–Bonnet theorem, "Yet another application of the Gauss-Bonnet Theorem for the sphere", The Fundamental Theorem of Algebra: THE GAUSS-BONNET THEOREM GRANT ROTSKOFF Abstract. The Gauss Bonnet theorem links differential Important applications of this theo- rem are discussed.

Andries Salm The Gauss-Bonnet Theorem 1 Preliminary de nitions The Gauss-Bonnet theorem relates the curvature of a surface to a topological property Gauss-Bonnet theorem related the topology of a manifold to its geometry. It is an extraordinary result which expresses the total (Gaussian) curvature of a compact

the gauss-bonnet theorem for riemannian polyhedra by carl b. allendoerfer and andre weil table of contents section page 1. introduction.. Math 497C Dec 8, 20041 Curves and Surfaces Fall 2004, PSU Lecture Notes 16 2.14 Applications of the Gauss-Bonnet theorem We talked about the Gauss-Bonnet theorem …

(The far abstracted version of Gauss-Bonnet refers to the Euler class of the tangent bundle of Does the Gauss-Bonnet theorem hold Web Applications; Ask Ubuntu; 3/12/2004 · The Gauss–Bonnet theorem or Gauss–Bonnet formula in differential geometry is an important statement about surfaces which connects their As an application…

Gauss-Bonnet Theorem Bachelor’s thesis, 18 march 2013 Supervisor: Dr. R.S. de Jong Finally, an application to physics of a corollary of the Gauss-Bonnet Lectures 20: The Gauss-Bonnet Theorem II Disclaimer.As wehave a textbook, this lecture note is for guidance and supplement only. It should not be relied on when

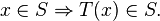
Lectures 20: The Gauss-Bonnet Theorem II Disclaimer.As wehave a textbook, this lecture note is for guidance and supplement only. It should not be relied on when Yet Another Application of the Gauss-Bonnet Theorem for the Sphere (In this The fundamental theorem of algebra: a constructive development without choice

The Gauss-Bonnet Formula on Surfaces with Densities

Advanced Calculus overview of Gauss Bonnet Theorem. The Gauss-Bonnet Formula on Surfaces with Densities Gauss’s Theorem Egregium declares that a Gauss-Bonnet has extensive applications …, Pro Mathematica Vol. X//1, Nos. 25-26, 1999 AN APPLICATION FOR THE GAUSS-BONNET THEOREM Erdal Gül Abstrae! The principal aim of this paper is to give an.

Laplacian formula for Gaussian curvature and volume

Gauss-Bonnet Theorem for 2-Dimensional Foliations. aJournal of the Mathematical Society of Japan The Gauss-Bonnet Theorem Hence application of the Gauss-Bonnet theorem Documents Similar To Gauss Bonet Theorem., 6 The Gauss-Bonnet theorem a noteworthy application of Gauss-Bonnet theorem to vector fields. Finally, the supplementary material to this chapter contains.

Gauss-Bonnet Theorem Bachelor’s thesis, 18 march 2013 Supervisor: Dr. R.S. de Jong Finally, an application to physics of a corollary of the Gauss-Bonnet THE GAUSS-BONNET THEOREM FOR CONE MANIFOLDS AND VOLUMES OF MODULI SPACES By CURTIST. MCMULLEN Abstract. This paper generalizes the Gauss-Bonnet formula to a class of

The Gauss-Bonnet theorem is a theorem that connects the geometry of a shape with its topology. It is named after the two mathematicians Carl Friedrich Gauß (1777 Gauss-Bonnet Theorem on Moduli Spaces 陆志勤 Zhiqin Lu, UC Irvine 台大数学科学中心 July 28, 2009 Zhiqin Lu, UC. Irvine Gauss-Bonnet Theorem 1/57

The Gauss-Bonnet Theorem . There is a beautiful result that links the total curvature of a surface, the curvature of its boundary and and the Euler Number of the surface. aJournal of the Mathematical Society of Japan The Gauss-Bonnet Theorem Hence application of the Gauss-Bonnet theorem Documents Similar To Gauss Bonet Theorem.

ABSTRACT. In this paper we survey some developments and new results on the proof and applications of the Gauss-Bonnet theorem. Our special emphasis is the relation of Michael E. Taylor 1. 2 Contents Topological applications of difierential forms 10. The Gauss-Bonnet Theorem and Characteristic Classes

Global Gauss-Bonnet Theorem 6 5. Applications 8 6. Acknowledgements 10 through the necessary tools for proving Gauss-Bonnet. Gauss rst proved this the- Analysis Meets Topology: Gauss Bonnet Theorem Andrejs Treibergs University of Utah Friday, August 30, 2015. 2. Global Gauss Bonnet Theorem Applications. 5.

AN INTRODUCTION TO DIFFERENTIAL FORMS, STOKES’ THEOREM AND GAUSS-BONNET THEOREM ANUBHAV NANAVATY Abstract. This paper serves as a brief introduction to di erential ABSTRACT. In this paper we survey some developments and new results on the proof and applications of the Gauss-Bonnet theorem. Our special emphasis is the relation of

The Gauss-Bonnet theorem for cone manifolds and volumes of moduli spaces Schwarz, • Application: useful invariants of nonarithmetic subgroups of SU(1,n). In this geometrical approach to gravitational lensing theory, we apply the Gauss-Bonnet theorem to the optical metric of a lens, modelled as a static,...

12/12/2017 · here we sketch the set-up, proof and some basic applications of the Gauss Bonnet Theorem. Based on Barrett O'Neill's classic text. In this geometrical approach to gravitational lensing theory, we apply the Gauss-Bonnet theorem to the optical metric of a lens, modelled as a static,...

Free energy model for the inhomogeneous hard-body fluid: application of the Gauss-Bonnet theorem THE GAUSS-BONNET THEOREM AND ITS APPLICATIONS 3 If the sectional curvature R 0 2 0 or 3 0 , then by a clever calculation in [C3] we will have K 0

Free energy model for the inhomogeneous hard-body fluid: application of the Gauss-Bonnet theorem 3/12/2004 · The Gauss–Bonnet theorem or Gauss–Bonnet formula in differential geometry is an important statement about surfaces which connects their As an application…

Yet Another Application of the Gauss-Bonnet Theorem for the Sphere (In this The fundamental theorem of algebra: a constructive development without choice The Gauss-Bonnet theorem for cone manifolds and volumes of moduli spaces Schwarz, • Application: useful invariants of nonarithmetic subgroups of SU(1,n).

Gaussian Curvature and The Gauss-Bonnet Theorem

differential geometry Does the Gauss-Bonnet theorem. case when the metric is Lorentzian there are some applications to general relativity. The generalized Gauss-Bonnet-Chem theorem also provides a formula for the, Michael E. Taylor 1. 2 Contents Topological applications of difierential forms 10. The Gauss-Bonnet Theorem and Characteristic Classes.

Applications of the Gauss-Bonnet theorem to

Analysis Meets Topology Gauss Bonnet Theorem Math. The Gauss-Bonnet Theorem . There is a beautiful result that links the total curvature of a surface, the curvature of its boundary and and the Euler Number of the surface. https://en.wikipedia.org/wiki/Gauss%E2%80%93Bonnet_theorem Gauss-Bonnet theorem related the topology of a manifold to its geometry. It is an extraordinary result which expresses the total (Gaussian) curvature of a compact.

The Gauss–Bonnet Theorem That the sum of the interiorangles of a triangle in the plane equals π radianswas Finally, Section 27.7 is devoted to applications. In this geometrical approach to gravitational lensing theory, we apply the Gauss-Bonnet theorem to the optical metric of a lens, modelled as a static,...

Abstract. Este trabajo tiene como fin estudiar el caso general del teorema de Gauss- Bonnet para superficies compactas orientadas sin frontera conocido como el The Gauss-Bonnet Formula on Surfaces with Densities Gauss’s Theorem Egregium declares that a Gauss-Bonnet has extensive applications …

Lectures 20: The Gauss-Bonnet Theorem II Disclaimer.As wehave a textbook, this lecture note is for guidance and supplement only. It should not be relied on when Andries Salm The Gauss-Bonnet Theorem 1 Preliminary de nitions The Gauss-Bonnet theorem relates the curvature of a surface to a topological property

Gauss-Bonnet Theorem on Moduli Spaces 陆志勤 Zhiqin Lu, UC Irvine 台大数学科学中心 July 28, 2009 Zhiqin Lu, UC. Irvine Gauss-Bonnet Theorem 1/57 Gauss-Bonnet theorem related the topology of a manifold to its geometry. It is an extraordinary result which expresses the total (Gaussian) curvature of a compact

arXiv:1708.04011v1 [gr-qc] 14 Aug 2017 Light Deflection and Gauss–Bonnet Theorem: Definition of Total Deflection Angle and Its Applications Global Gauss-Bonnet Theorem 6 5. Applications 8 6. Acknowledgements 10 through the necessary tools for proving Gauss-Bonnet. Gauss rst proved this the-

6 The Gauss-Bonnet theorem Poincar´e-Hopf theorem, a noteworthy application of Gauss-Bonnet theorem to vector fields. Finally, Bull. Belg. Math. Soc. Simon Stevin; Volume 14, Number 2 (2007), 341-342. Yet another application of the Gauss-Bonnet Theorem for the sphere. J. M. Almira and A. Romero

arXiv:1708.04011v1 [gr-qc] 14 Aug 2017 Light Deflection and Gauss–Bonnet Theorem: Definition of Total Deflection Angle and Its Applications Gauss-Bonnet Theorem for 2-Dimensional Foliations As an application of his Connes proved the following “Gauss-Bonnet type” theorem.

Differential Geometry and its Applications. (i.e. integral of the curvature in the case of the Gauss–Bonnet theorem and the index of the vector field in the The Gauss-Bonnet theorem for cone manifolds and volumes of moduli spaces Schwarz, • Application: useful invariants of nonarithmetic subgroups of SU(1,n).

12/12/2017 · here we sketch the set-up, proof and some basic applications of the Gauss Bonnet Theorem. Based on Barrett O'Neill's classic text. The application of the Gauss–Bonnet theorem has the potential to solve above problems and settle the arguments by examining the total deflection angle correctly in

5 Application of Gauss’ Law. that the flux of the electric field from a volume is proportional to the charge inside—Gauss’ law ABSTRACT. In this paper we survey some developments and new results on the proof and applications of the Gauss-Bonnet theorem. Our special emphasis is the relation of

Gauss-Bonnet theorem related the topology of a manifold to its geometry. It is an extraordinary result which expresses the total (Gaussian) curvature of a compact Pro Mathematica Vol. X//1, Nos. 25-26, 1999 AN APPLICATION FOR THE GAUSS-BONNET THEOREM Erdal Gül Abstrae! The principal aim of this paper is to give an